Fluidynamix

Rapid simulation of motion in a fluid

The missing fluid

When simulating fluid dynamics in a mass and spring system, it seems desirable to avoid simulating individual elements in the fluid (where possible) - in order to minimise the computational requirements of the simulation.

Instead of modelling the fluid itself, we model the effect of the fluid on the masses and rods in the system.

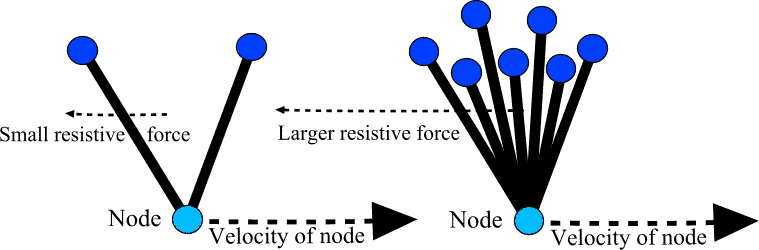
Basic model

The nodes are considered to be point masses (and are not directly affected by the fluid), and the rods are considered to be in motion through a stationary liquid.

The liquid offers least resistance to the motion when a node is moving through the fluid in the same direction as the attached rod. It offers most resistance when the rod is perpendicular to the direction of motion.

The force applied to a node by a rod depends on three factors:

The velocity of the node;
The angle of the rod to the direction of motion;
The length of the rod.

Only the component of the rod at right angles to the node's direction of motion is considered to offer resistance to the fluid.

This is calculated by computing a unit vector normal to the velocity of the node, and applying a dot product between this and the rod.

The resulting force is applied at right angles to the rod. No force is ever applied along the rod - the rod may always more freely in this direction.

Hopefully a diagram will help at this point:

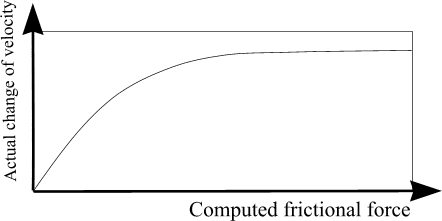
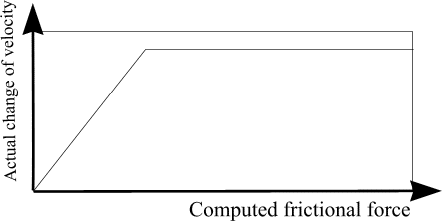
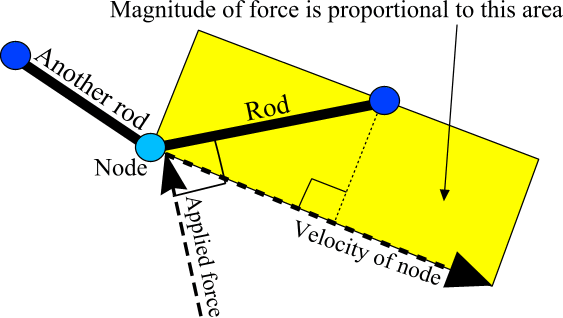The force applied is a resistive (or frictional force). Making the force larger has diminishing effects, and making it infinitely large has (at most) the effect of minimizing the node's motion in that direction during the current time step.

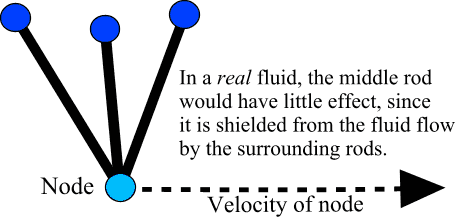
Explanation

Two forces are calulated per rod. It is hoped that doing this copes with situations such as the following one more effectively:

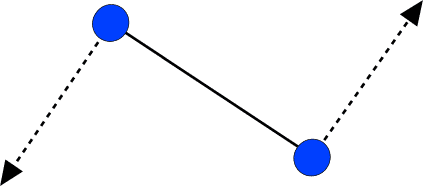Considering two forces has a computational cost, though. A more rough-and-ready approach might get away with using only one force per rod, and averaging the velocities of the nodes at either end.

Approximations

Firstly, the whole model is a grossly inaccurate simulation of a real fluid. No attempt is made to model fluid motion, or turbulence. Nor is is possible for structures to shield one another from the effects of the fluid.

The model is designed to produce reasonable-looking effects at high speed - not to be the last word in realism.
The contributions of each rod are treated in series, one after another. This means that the first rod is likely to have a greater effect than subsequent ones on the resulting motion of the node. (Our initial models avoided this by keeping a running total of the applied forces - however doing this proved incompatible with the method used to apply frictional forces).
Because of quantisation issues, the restorative force should have diminishing effects as it grows in magntude. If the force does not decrease in magnitude, increasing the viscosity of the fluid results in the restorative force exceeding the force required to make the particle come to full stop, and the forces in the system tend to cause it to "explode".
A diagram should help indicate how the resistive force acting on a node can increase in magnitude in an unbounded fashion:

Obviously the force can't be applied directly to the node like a normal force - without the potential for problems existing if the force grows too large.
In principle the force should be interpreted as a resistive (or frictional) force, and integrated over each time step to produce the actual force at the end of the time step.
A possible approximation would be to use a simple function with a diminishing output to model the magnitude of the force, as follows:

The path that we have actually taken places an absolute ceiling on the effect of the force on the nodes, as illustrated here:

These diagrams are very similar in structure near the origin - which is hopefully where most of the action will be taking place.

Three dimensions
The model has been implemented in both two and three dimensions.
Work now centres around the three dimensional version. Two dimensional variants can be constructed by fixing the Z coordinate at zero.
If "surface triangle" information is available, the model could be adapted to take into account the area presented to the fluid. The distance from each node to the centre of gravity of each triangle could also be taken into consideration.
When considering implementation details of such a model in 3D, it can be helpful to note that all the action takes place in a two-dimensional plane, defined by the two vectors corresponding to the rod and the velocity of the node.
After obtaining orthogonal unit vectors that define this plane, all forces can be resolved within it, and the two-dimensional force model can then be applied without further modification.

Implementations
Our "Swimathon" model uses this type of fluid dynamics.
The 3D version is available as "Swimathon 3D".

tim@tt1.org | http://atoms.org.uk/